What is Data Science?
Welcome to the dynamic realm of Data Science—a continuous process rather than a singular event. At its core, Data Science is the systematic exploration of data to gain profound insights into diverse aspects of the world. It involves crafting models or hypotheses, using data to validate them, and ultimately translating data into compelling stories. It's the art of uncovering hidden trends and narratives that drive strategic decision-making for companies and institutions.
In essence, Data Science revolves around processes and systems to extract meaningful information from both structured and unstructured data forms. Similar to how biological sciences delve into biology or physical sciences study physical reactions, Data Science is the dedicated study of data—real and possessing intrinsic properties that demand exploration.
Fundamentals of Data Science
Defining Data Science can be subjective, with varying interpretations, but a common thread is its significant focus on data analysis. While data analysis itself isn't a novel concept, the unprecedented wealth of data from diverse sources, such as log files, social media, sales records, and more, distinguishes the contemporary landscape. The surge in available data coincides with enhanced computing power, enabling meaningful analyses and the discovery of new insights.
Data Science serves as a catalyst for organizations seeking to comprehend their surroundings, tackle existing challenges, and unveil untapped opportunities. Data scientists leverage data analysis to augment organizational knowledge, delving into data to determine how it can best contribute value to the business. So, what is the procedural essence of data science?
Many organizations employ data science to address specific issues, emphasizing the importance of clearly defining the question at hand. This initial step shapes the trajectory of the entire data science project. A key trait of adept data scientists is curiosity—they pose questions to precisely understand the business need. The subsequent inquiries revolve around identifying the necessary data and its sources. Data scientists adeptly analyze both structured and unstructured data, choosing diverse approaches based on the nature of the problem.
Utilizing various models to scrutinize data uncovers patterns and anomalies. Sometimes, these findings validate existing assumptions, but often they present entirely new insights, guiding organizations toward innovative strategies. As the data discloses its revelations, the data scientist transitions into the role of a storyteller, effectively communicating results to project stakeholders. Leveraging advanced data visualization tools, data scientists help stakeholders grasp the significance of the results and determine recommended courses of action.
In essence, Data Science is a transformative force, reshaping how we work, how we harness data, and how organizations perceive and navigate the world. The synergy of data analysis, curiosity-driven exploration, and effective communication positions Data Science as a key player in driving organizational evolution.
The term "Data Science" emerged in the 80s and 90s when visionary professors sought to redefine the statistics curriculum. However, beyond nomenclature, Data Science is fundamentally an individual's endeavor to work with data, seeking answers to questions through exploration, manipulation, and analysis. It's more about the data itself than a strict adherence to scientific principles.
Today, Data Science holds immense relevance due to the abundance of available data—what was once a concern for data scarcity has transformed into a data deluge. With the evolution of algorithms, the widespread availability of open-source software, and cost-effective storage solutions, the tools for working with data are not only accessible but ubiquitous. This era presents an unprecedented opportunity for aspiring data scientists. If you possess curiosity and engage in the exploration, manipulation, and analysis of data, you are, in essence, practicing Data Science.
Join us in this exciting era where the tools, data availability, and analytical capabilities converge, making it an unparalleled time to be a data scientist. Explore the endless possibilities that Data Science offers and seize the opportunities that come with navigating this data-rich landscape. Welcome to the era where data meets exploration, and insights shape the future.
What is Machine Learning?
Machine Learning (ML) has become ubiquitous across diverse fields and industries, showcasing its transformative impact on various applications. One prominent domain where ML thrives is in the self-driving car industry, where it plays a crucial role in classifying objects encountered during driving, such as people, traffic signs, and other vehicles.
Major cloud computing service providers like IBM and Amazon harness machine learning to enhance security measures. ML is instrumental in detecting and preventing cyber threats, including distributed denial-of-service attacks and identifying suspicious or malicious usage patterns.
Financial sectors leverage ML for analyzing stock data, unveiling trends, and identifying patterns that inform strategic decisions on stock trading. In the realm of healthcare, ML contributes significantly to medical diagnostics. For instance, it aids in the early detection of potential tumors in patients using technologies like x-ray scans.
The course at hand comprises four comprehensive modules designed to equip learners with fundamental ML concepts and practical skills. These modules are:
1. Introduction and Regression:
- Understand the basics of ML and delve into linear regression.
- Apply ML algorithms to estimate and predict outcomes, such as predicting CO2 emissions of cars using an automobile dataset.
2. Classification:
- Explore classification algorithms, such as logistic regression and k-nearest neighbors.
- Utilize ML for predicting customer loyalty based on telecommunication customer data.
3. Clustering:
- Learn about clustering through techniques like support vector machines and decision trees.
- Apply ML to classify human cell samples and determine which drugs to prescribe to patients.
Throughout the course, hands-on labs using Jupyter Lab and Python programming language, along with libraries like Pandas, Numpy, and Scikit-Learn, provide practical experience. Learners engage with different datasets, applying ML algorithms to tasks like predicting house prices, customer loyalty, and medical conditions.
Upon completion, participants gain the ability to:
- Explain, compare, and contrast ML concepts, including supervised and unsupervised learning.
- Understand key ML algorithms and their applications in diverse scenarios.
- Apply ML algorithms using Python and relevant libraries, enhancing their proficiency in real-world problem-solving.
By delving into the fundamentals of ML and its practical applications, this course empowers learners to navigate the dynamic landscape of machine learning, making them adept at leveraging these powerful tools in a variety of contexts.
In the healthcare sector, discover how data scientists utilize Machine Learning to predict the nature of human cells, aiding in the early detection of potential cancer risks. This not only contributes to medical diagnoses but also plays a pivotal role in safeguarding individual health and well-being.
Explore the invaluable role of decision trees, demonstrating how constructing effective decision trees from historical data assists doctors in tailoring precise medicine prescriptions for their patients. The course further delves into the financial domain, showcasing how Machine Learning guides bankers in making informed decisions regarding loan approvals and intricate tasks like bank customer segmentation, particularly challenging with vast and diverse datasets.
Uncover the secrets behind recommendation systems on popular websites like YouTube, Amazon, and Netflix. Understand how Machine Learning powers these platforms to provide personalized recommendations for movies, books, and various products. The possibilities with Machine Learning are vast, and in this course, you'll harness the power of popular Python libraries.
Using examples like estimating CO2 emissions in automobiles with scikit-learn, you'll gain hands-on experience in building predictive models. The course extends into predicting future CO2 emissions for yet-to-be-produced cars and exploring how telecommunications industries leverage Machine Learning to foresee customer churn.
The course features a user-friendly lab environment, eliminating the need for installations or cloud setups. By simply clicking a button, you can initiate the lab environment in your browser. The provided Python code, embedded in Jupyter notebooks, allows you to run, modify, and understand algorithms effortlessly.
What can you achieve by undertaking this course? Dedicate a few hours each week over the coming weeks, and you'll acquire valuable skills to augment your resume. From regression and classification to clustering, scikit-learn, and psy PI, you'll master a diverse set of skills. Additionally, you'll undertake hands-on projects, including cancer detection, economic trend prediction, customer churn forecasting, and recommendation engines, enhancing your portfolio. Upon completion, you'll receive a Machine Learning certificate, providing tangible proof of your competence, which you can showcase on platforms like LinkedIn and social media.
Welcome to the "Machine Learning with Python" Course: Understanding the Power of Machine Learning
In this course, we embark on a journey into the world of Machine Learning (ML) and its transformative applications across diverse fields. Let's delve into a scenario where a human cell sample's characteristics become pivotal in determining whether it's benign or malignant. Early diagnosis of malignant cells is critical for a patient's survival, and ML becomes the tool that aids in this process.
Machine Learning Defined:
ML is a subfield of computer science that grants computers the ability to learn without explicit programming. Unlike traditional methods where rules were predefined, ML allows computers to iteratively learn patterns from data, mirroring the way humans learn and understand the world.
Real-Life Impact of Machine Learning:
Explore how ML influences various aspects of society. From Netflix and Amazon's personalized recommendations to banks predicting loan approval probabilities, ML is omnipresent. Telecommunication companies leverage ML to predict customer behavior, while anomaly detection aids in credit card fraud prevention. The application of ML extends to chatbots, face recognition, and even computer games.
Popular ML Techniques:
Dive into some widely used ML techniques:
- Regression/Estimation:Predicting continuous values like house prices or CO2 emissions.
- **Classification:** Determining the class or category of a case, e.g., benign or malignant cells.
- **Clustering:** Grouping similar cases, relevant for customer segmentation.
- **Association:** Discovering co-occurring items or events, as seen in grocery shopping patterns.
- **Anomaly Detection:** Identifying abnormal cases, such as credit card fraud detection.
- **Sequence Mining:** Predicting the next event, like website click-streams.
- **Dimension Reduction:** Reducing data size.
- **Recommendation Systems:** Associating preferences and recommending items like books or movies.
**Demystifying Buzzwords: AI vs. ML vs. Deep Learning:**
Understand the distinctions between Artificial Intelligence (AI), ML, and Deep Learning. AI encompasses a broad scope, while ML is its statistical component, focusing on problem-solving through learning from examples. Deep Learning takes ML to a new level, enabling computers to make intelligent decisions autonomously.
Python for Machine Learning
**Exploring Essential Python Libraries for Data Science and Machine Learning**
Python stands out as a versatile and potent general-purpose programming language, increasingly becoming the preferred choice among data scientists. This course aims to introduce and leverage key Python packages, streamlining the implementation of machine-learning algorithms and enhancing your hands-on experience.
**1. NumPy:**
NumPy is a fundamental math library designed for working with N-dimensional arrays in Python. It significantly enhances computational efficiency and effectiveness, surpassing regular Python capabilities. Understanding NumPy is crucial for tasks involving arrays, dictionaries, functions, data types, and image processing.
**2. SciPy:**
SciPy is a comprehensive library housing numerical algorithms and domain-specific toolboxes, spanning signal processing, optimization, statistics, and more. Ideal for scientific and high-performance computation, SciPy provides valuable resources for data scientists tackling real-world problems.
**3. Matplotlib:**
Matplotlib, a widely used plotting package, offers both 2D and 3D plotting capabilities. This package is essential for visualizing data and patterns, providing a powerful tool for data scientists to communicate insights effectively.
**4. Pandas:**
Pandas is a high-level Python library designed for efficient and user-friendly data manipulation. With functions tailored for data importing, manipulation, and analysis, Pandas simplifies tasks related to numerical tables and time series, proving invaluable for data scientists.
**5. SciKit Learn:**
SciKit Learn takes center stage as a free Machine Learning Library for Python, featuring a plethora of classification, regression, and clustering algorithms. Built to seamlessly integrate with Python's numerical and scientific libraries (NumPy and SciPy), SciKit Learn streamlines the machine-learning process. Its user-friendly interface allows for easy implementation with minimal lines of code, covering tasks such as preprocessing, feature selection, model training, evaluation, and more.
**Example with SciKit Learn:**
A glimpse into using SciKit Learn showcases its simplicity. Standardizing datasets, splitting them into train and test sets, setting up algorithms, training models, making predictions, evaluating accuracy using metrics like confusion matrices, and saving models—all accomplished effortlessly with just a few lines of code.
**Course Overview:**
This course provides an in-depth exploration of these essential Python libraries, offering insights into their applications and practical usage. Whether you're a beginner or seeking to enhance your data science skills, this course is tailored to provide a comprehensive understanding of the tools necessary for success in the field.
**Conclusion:**
While machine-learning terms may initially seem complex, this course aims to demystify them, guiding you through each step in subsequent videos. Keep in mind that the power of SciKit Learn lies in its ability to simplify the entire machine-learning process, enabling efficient and effective implementation with minimal coding effort. Stay tuned for a deep dive into these essential Python libraries, and thank you for watching.
Supervised vs Unsupervised
**Supervised vs. Unsupervised Learning: A Comprehensive Exploration**
Machine learning can be broadly categorized into two main types: supervised learning and unsupervised learning. Each approach addresses different aspects of data analysis and pattern recognition, offering unique advantages and use cases. Let's delve into the details of both supervised and unsupervised learning, accompanied by illustrative examples.
### **Supervised Learning:**
**Definition:**
Supervised learning involves training a model on a labeled dataset, where the algorithm learns to map input features to the corresponding output labels. The goal is to teach the model to make accurate predictions or decisions when given new, unseen data.
**Key Characteristics:**
- **Labeled Data:** The training dataset includes input-output pairs, providing the algorithm with labeled examples.
- **Objective:** The model aims to learn the mapping function from inputs to outputs, optimizing for accurate predictions.
- **Feedback Mechanism:** The algorithm receives feedback during training, allowing it to adjust its parameters for improved performance.
**Examples:**
1. **Classification:** Predicting whether an email is spam or not based on features like sender, subject, and content.
2. **Regression:** Estimating the price of a house based on features like square footage, number of bedrooms, and location.
### **Unsupervised Learning:**
**Definition:**
Unsupervised learning involves training a model on an unlabeled dataset, and the algorithm must discover patterns or structures within the data without explicit guidance on the output.
**Key Characteristics:**
- **Unlabeled Data:** The training dataset lacks output labels, and the algorithm must infer patterns or groupings.
- **Objective:** The model aims to identify inherent structures, relationships, or clusters within the data.
- **Limited or No Feedback:** Without explicit labels, the algorithm operates with minimal guidance, making it exploratory.
**Examples:**
1. **Clustering:** Grouping customers based on purchasing behavior without predefined categories.
2. **Dimensionality Reduction:** Reducing the number of features while retaining essential information for easier analysis.
3. **Association:** Discovering patterns like items frequently purchased together in a retail transaction dataset.
### **Comparison:**
**Use Cases:**
- **Supervised Learning:** Ideal for tasks requiring prediction, classification, or regression when labeled training data is available.
- **Unsupervised Learning:** Suited for tasks where the goal is to explore and discover patterns, relationships, or groupings in data.
**Algorithmic Differences:**
- **Supervised Learning:** Algorithms include decision trees, support vector machines, and neural networks.
- **Unsupervised Learning:** Algorithms encompass k-means clustering, hierarchical clustering, and principal component analysis (PCA).
**Challenges:**
- **Supervised Learning:** Dependency on labeled data, which may require extensive human effort for annotation.
- **Unsupervised Learning:** Ambiguity in evaluating results, as there are no explicit output labels for validation.
**Hybrid Approaches:**
- **Semi-Supervised Learning:** Combines elements of both supervised and unsupervised learning, leveraging a small amount of labeled data and a larger pool of unlabeled data.
### **Conclusion:**
In summary, the choice between supervised and unsupervised learning depends on the nature of the task and the availability of labeled data. Supervised learning excels in predictive tasks with clear outcomes, while unsupervised learning proves valuable for exploring data structures and relationships in an unsupervised manner. Understanding the distinctions between these approaches is essential for choosing the most suitable methodology for a given machine learning task.
Regression
**Regression: A Comprehensive Overview with Practical Examples**
Regression is a fundamental concept in statistical modeling and machine learning, serving as a powerful tool for predicting continuous outcomes based on input variables. In this detailed note, we'll delve into the essence of regression, its types, key components, and provide practical examples to illustrate its application.
### **I. Understanding Regression: The Core Concept**
At its core, regression involves establishing a relationship between dependent and independent variables. The goal is to model this relationship, enabling the prediction of a continuous target variable based on one or more predictor variables. The underlying assumption is that there exists a linear or nonlinear association between the variables.
### **II. Types of Regression: A Spectrum of Approaches**
1. **Linear Regression:**
- *Overview:* Assumes a linear relationship between variables.
- *Equation:* y = β0 +β1x+ε
- *Example:* Predicting house prices based on square footage.
2. **Multiple Linear Regression:**
- *Overview:* Extension of linear regression to multiple predictors.
- *Equation:* y i =β 0 +β 1 x i1 +β 2 x i2 +...+β p x ip +ϵ
where, for i=n observations:
yi =dependent variable
xi =explanatory variables
β0 =y-intercept (constant term)
βp =slope coefficients for each explanatory variable
ϵ=the model’s error term (also known as the residuals)
*Example:* Forecasting a student's GPA considering study hours, attendance, etc.
3. **Polynomial Regression:**
- *Overview:* Accommodates polynomial relationships.
- *Equation:* \(Y = \beta_0 + \beta_1X + \beta_2X^2 + ... + \beta_nX^n + \epsilon\).
- *Example:* Modeling growth patterns in biology.
4. **Ridge Regression (L2 Regularization):**
- *Overview:* Mitigates multicollinearity by penalizing large coefficients.
- *Equation:* Incorporates a regularization term in the loss function.
5. **Lasso Regression (L1 Regularization):**
- *Overview:* Encourages sparsity in the coefficient matrix.
- *Equation:* Adds the absolute values of coefficients to the loss function.
### **III. Key Components of Regression Analysis**
1. **Dependent Variable (Y):** The target variable to be predicted.
2. **Independent Variables (X):** The predictors influencing the dependent variable.
3. **Coefficients (\(\beta\)):** Parameters determining the strength and direction of the relationship.
4. **Residuals (\(\epsilon\)):** The differences between predicted and observed values.
5. **Loss Function:** Measures the model's predictive performance.
6. **Training and Testing Sets:** Data division for model training and evaluation.
### **IV. Practical Examples: Bringing Regression to Life**
1. **Linear Regression Example: Predicting Exam Scores**
- *Data:* Student study hours vs. exam scores.
- *Outcome:* Predicting exam scores based on study hours.
2. **Multiple Linear Regression Example: House Price Prediction**
- *Data:* Features like square footage, bedrooms, bathrooms.
- *Outcome:* Predicting house prices.
3. **Polynomial Regression Example: Growth Pattern Modeling**
- *Data:* Biological growth data.
- *Outcome:* Capturing complex growth patterns.
### **V. Evaluation Metrics in Regression**
1. **Mean Squared Error (MSE):** Measures average squared differences between predicted and actual values.
2. **R-squared (R²):** Indicates the proportion of variance explained by the model.
### **VI. Conclusion: Regression's Ubiquity and Power**
Regression, in its various forms, stands as a cornerstone in predictive modeling. From linear relationships to intricate polynomial patterns, regression equips data scientists with the tools to uncover insights and make accurate predictions. Whether forecasting exam scores or housing prices, regression's versatility and interpretability make it an invaluable asset in the data science toolkit.
Model Evaluation in Regression Models
import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
y_true = np.array([300000, 400000, 500000, 600000, 700000])
y_pred = np.array([310000, 390000, 510000, 590000, 710000])
1. Mean Absolute Error (MAE):
- The mean absolute error is the average absolute difference between predicted and actual values.
mae = mean_absolute_error(y_true, y_pred)
print(f"Mean Absolute Error (MAE): {mae}")
2. **Mean Squared Error (MSE):**
- The mean squared error is the average of the squared differences between predicted and actual values.
mse = mean_squared_error(y_true, y_pred)
print(f"Mean Squared Error (MSE): {mse}")
3. **Root Mean Squared Error (RMSE):**
- The square root of the MSE.
rmse = np.sqrt(mse)
print(f"Root Mean Squared Error (RMSE): {rmse}")
```
4. R-squared (R²):
- R-squared is a measure of how well the model explains the variance in the data.
r2 = r2_score(y_true, y_pred)
print(f"R-squared (R²): {r2}")
5. Adjusted R-squared:
- Adjusted R-squared accounts for the number of predictors in the model.
# Assuming you have the number of predictors (p) in your model
p = 2 # Replace with the actual number of predictors
n = len(y_true)
adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
print(f"Adjusted R-squared: {adjusted_r2}")
These metrics provide different perspectives on the model's performance. A lower MAE, MSE, and RMSE are desirable, while a higher R-squared and adjusted R-squared indicate a better fit. Always consider the specific goals and characteristics of your regression problem when interpreting these metrics. Additionally, visualizing residuals and using cross-validation are valuable steps in model evaluation.
Model Evaluation in Regression Models
Model evaluation is a critical step in assessing the performance of regression models. It helps us understand how well the model generalizes to new, unseen data. In this note, we'll explore different approaches to evaluate regression models, with a focus on Train/Test Split and K-fold Cross-Validation.
Train/Test Split
One common method for evaluating regression models is the train/test split. In this approach, the dataset is divided into training and testing sets. The model is trained on the training set and then tested on the separate testing set. This ensures a more accurate evaluation of out-of-sample accuracy.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Assuming X and y are your feature and target variables
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Initialize and train the model
model = LinearRegression()
model.fit(X_train, y_train)
# Make predictions on the test set
predictions = model.predict(X_test)
# Evaluate the model
mse = mean_squared_error(y_test, predictions)
print(f"Mean Squared Error (MSE): {mse}")
K-fold Cross-Validation
Train/test split has limitations, such as dependency on the specific split. K-fold Cross-Validation addresses this by performing multiple train/test splits, averaging the results for a more consistent out-of-sample accuracy.
from sklearn.model_selection import cross_val_score, KFold
# Assuming X and y are your feature and target variables
kf = KFold(n_splits=4, shuffle=True, random_state=42)
# Initialize the model
model = LinearRegression()
#Perform K-fold cross-validation
cv_results = cross_val_score(model, X, y, cv=kf, scoring='neg_mean_squared_error')
Calculate mean squared error from cross-validation results
mse_cv = -np.mean(cv_results)
print(f"Mean Squared Error (CV): {mse_cv}")
Examples
Let's consider a simple example with a housing dataset. The goal is to predict house prices based on features like square footage, number of bedrooms, and location.
Train/Test Split Example:
# Assuming df is your housing dataset
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
X = df.drop('price', axis=1)
y = df['price']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = LinearRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
mse = mean_squared_error(y_test, predictions)
print(f"Mean Squared Error (Test Set): {mse}")
K-fold Cross-Validation Example:
# Assuming df is your housing dataset
from sklearn.model_selection import cross_val_score, KFold
from sklearn.linear_model import LinearRegression
X = df.drop('price', axis=1)
y = df['price']
kf = KFold(n_splits=4, shuffle=True, random_state=42)
model = LinearRegression()
cv_results = cross_val_score(model, X, y, cv=kf, scoring='neg_mean_squared_error')
mse_cv = -np.mean(cv_results)
print(f"Mean Squared Error (Cross-Validation): {mse_cv}")
In these examples, we've demonstrated the implementation of train/test split and K-fold cross-validation for model evaluation. These techniques help ensure that our regression model performs well on unseen data, providing more robust and reliable results.
Accuracy metrics for model Evaluation
In regression models, several evaluation metrics are commonly used to assess the performance and accuracy of the model in predicting continuous outcomes. Here are some key evaluation metrics for regression models:
1. **Mean Absolute Error (MAE):**
- Measures the average absolute difference between the predicted and actual values.
- Formula: \[ MAE = \frac{1}{n} \sum_{i=1}^{n} |y_{i} - \hat{y}_{i}| \]
2. **Mean Squared Error (MSE):**
- Measures the average squared difference between the predicted and actual values.
- Formula: \[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^2 \]
3. **Root Mean Squared Error (RMSE):**
- Represents the square root of the mean squared error, providing a more interpretable scale.
- Formula: \[ RMSE = \sqrt{MSE} \]
4. **R-squared (R²):**
- Indicates the proportion of the variance in the dependent variable that is predictable from the independent variables.
- R² ranges from 0 to 1, where 1 indicates a perfect fit.
- Formula: \[ R^2 = 1 - \frac{\sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^2}{\sum_{i=1}^{n} (y_{i} - \bar{y})^2} \]
5. **Adjusted R-squared:**
- Adjusts R² for the number of predictors in the model, providing a more realistic measure.
- Formula: \[ Adjusted \, R^2 = 1 - \frac{(1 - R^2)(n - 1)}{n - p - 1} \]
where \( n \) is the number of observations and \( p \) is the number of predictors.
6. **Mean Squared Logarithmic Error (MSLE):**
- Measures the mean squared logarithmic difference between the predicted and actual values, useful for models where the target variable has exponential growth.
- Formula: \[ MSLE = \frac{1}{n} \sum_{i=1}^{n} (\log(1 + y_{i}) - \log(1 + \hat{y}_{i}))^2 \]
7. **Mean Absolute Percentage Error (MAPE):**
- Calculates the average percentage difference between the predicted and actual values, expressed as a percentage.
- Formula: \[ MAPE = \frac{1}{n} \sum_{i=1}^{n} \left| \frac{y_{i} - \hat{y}_{i}}{y_{i}} \right| \times 100 \]
8. **Root Mean Squared Logarithmic Error (RMSLE):**
- Represents the square root of the mean squared logarithmic error, often used when the target variable has exponential growth.
- Formula: \[ RMSLE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\log(1 + y_{i}) - \log(1 + \hat{y}_{i}))^2} \]
When evaluating regression models, it's essential to consider the specific characteristics of your data and the goals of your analysis. Different metrics may be more suitable depending on the nature of the problem and the importance of specific types of errors.
Multiple Linear Regression (MLR):
Multiple Linear Regression (MLR):
Definition:
MLR is a statistical technique that models the linear relationship between a single dependent variable (also called response variable) and multiple independent variables (also called predictor variables or features).
It's an extension of simple linear regression, which only considers one independent variable.
The goal of MLR is to find the best-fitting equation that describes how changes in the independent variables affect the dependent variable.
Equation:
The general equation for MLR is:
Y = β0 + β1X1 + β2X2 + ... + βpXp + ε
Where:
Y = dependent variable
X1, X2, ..., Xp = independent variables
β0 = intercept (value of Y when all X's are 0)
β1, β2, ..., βp = regression coefficients (representing the change in Y for a unit change in each X)
ε = error term (accounting for unexplained variability)
Assumptions:
Linearity: The relationship between the dependent variable and independent variables is linear.
Independence: The observations are independent of each other.
Normality: The error terms are normally distributed.
Homoscedasticity: The variance of the error terms is constant across all levels of the independent variables.
No multicollinearity: Independent variables are not highly correlated with each other.
Estimation of Coefficients:
The most common method for estimating the regression coefficients (β) is the Ordinary Least Squares (OLS) method. It aims to minimize the sum of squared residuals (the differences between the actual and predicted values of Y).
Evaluation:
R-squared: Measures the proportion of variance in the dependent variable explained by the independent variables.
Adjusted R-squared: Adjusted version of R-squared that penalizes for the number of independent variables.
F-test: Tests the overall significance of the regression model.
t-tests: Test the significance of individual regression coefficients.
Applications:
Used extensively in various fields, including:
Economics (e.g., predicting sales based on advertising, price, and other factors)
Finance (e.g., predicting stock prices based on financial indicators)
Medicine (e.g., predicting patient outcomes based on medical history and test results)
Marketing (e.g., predicting customer behavior based on demographics and purchase history)
Social sciences (e.g., investigating relationships between social factors)
Engineering (e.g., modeling system performance based on design parameters)
Implementation in Python:
Libraries like scikit-learn provide tools for building and evaluating MLR models:
Python
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train) # Train the model
predictions = model.predict(X_test) # Make predictions
Use code with caution. Learn more
Key Considerations:
Feature selection: Choosing relevant independent variables is crucial.
Model validation: Ensure the model generalizes well to new data.
Outliers and influential points: Identify and handle outliers and data points that have undue influence on the model.
Violations of assumptions: Assess and address potential violations of MLR assumptions.
Building the Framework:
Problem Definition: Identify the target variable (what you want to predict) and the predictor variables (what you think influences it). Ensure all are continuous numeric variables or converted before proceeding.
Model Equation:
General Form: Y = β₀ + β₁X₁ + β₂X₂ + ... + βₙXₙ + ε
Y: Dependent variable
X₁...Xₙ: Independent variables
β₀: Intercept (Y value when all X's are 0)
β₁...βₙ: Regression coefficients (change in Y for a unit change in each X)
ε: Error term (unexplained variability)
Assumptions:
Linearity: Relationship between Y and X is linear. Visualize with scatter plots.
Independence: Observations are independent of each other.
Normality: Error terms are normally distributed. Check with Q-Q plots or normality tests.
Homoscedasticity: Error variance is constant across X levels. Assess visually or statistically.
No Multicollinearity: Independent variables are not highly correlated (affects coefficient interpretations). Check with correlation matrices or VIF values.
Estimating the Coefficients:
Ordinary Least Squares (OLS): Minimizes the sum of squared residuals (differences between predicted and actual Y values) to find the best-fitting line (hyperplane) for the data. Popular method, but computationally expensive for large datasets.
Optimization Algorithms: Iteratively minimize the error by adjusting the coefficients, often more efficient for large datasets. Gradient descent is a common example.
Evaluating the Model:
R-squared: Measures the proportion of variance in Y explained by the model. Higher values (closer to 1) indicate better fit.
Adjusted R-squared: Penalizes for the number of independent variables, providing a more reliable estimate of fit for multiple regression.
F-test: Tests the overall significance of the regression model. A p-value < 0.05 indicates the model is statistically significant.
t-tests: Test the significance of individual regression coefficients. A p-value < 0.05 indicates the coefficient is significantly different from zero, meaning the corresponding variable contributes significantly to the prediction of Y.
Interpretation and Application:
Analyze the regression coefficients:
Positive β indicates a direct relationship between the variable and Y (increases Y with increased X).
Negative β indicates an inverse relationship (decreases Y with increased X).
Magnitude of β represents the relative strength of the relationship.
Use the model to predict Y for new data points with similar characteristics.
Be aware of limitations:
Only estimates linear relationships. Requires checking assumptions and potential non-linearity.
Overfitting can occur with too many variables, leading to poor generalization.
Consider techniques like variable selection and regularization to address issues like multicollinearity and overfitting.
Additional Resources:
Python libraries like scikit-learn provide tools for building and evaluating multiple linear regression models.
Further exploration includes non-linear regression techniques for situations where linearity assumptions are not met.
This detailed explanation should provide a more comprehensive understanding of multiple linear regression, including its underlying assumptions, estimation methods, evaluation metrics, and practical applications. Remember, adapting the model to your specific data and addressing potential limitations are crucial for reliable analysis and prediction.
I. Understanding Classification:
Goal: Assign data points to predefined categories (classes) based on learned relationships between features and those classes.
Types:
Binary Classification: Two possible classes (e.g., spam/not spam, loan default/no default).
Multi-class Classification: More than two classes (e.g., handwritten digit recognition, medication response prediction).
II. How Classifiers Work:
Training:
Provide a classifier with labeled training data (data points with known class labels).
The classifier learns patterns and rules to distinguish between classes.
Prediction:
Present an unlabeled data point (test case) to the trained classifier.
The classifier predicts the most likely class label for that new data point.
III. Business Applications:
Customer segmentation
Churn detection
Predicting responses to marketing campaigns
Fraud detection
Risk assessment
Medical diagnosis
Image and text classification
IV. Common Classification Algorithms:
Decision trees
Naive Bayes
Linear discriminant analysis
K-nearest neighbor
Logistic regression
Neural networks
Support vector machines
V. Broad Applicability:
Classification can be applied to diverse problems across industries where labeled data is available and associations between features and target variables can be learned.
VI. Further Exploration:
Explore specific classification algorithms in more depth.
Understand advanced techniques like feature engineering and ensemble methods.
Consider ethical implications of classification models and data bias.
K-Nearest Neighbours
1. Understanding KNN:
A classification algorithm that classifies new data points based on their similarity to existing data points.
It assumes that similar data points are close to each other in the feature space.
2. How KNN Works:
Choose a value for K: This is the number of nearest neighbors to consider.
Calculate distance to neighbors: Measure the distance between the new data point and each existing data point in the training set.
Identify K nearest neighbors: Find the K data points with the smallest distances to the new data point.
Predict class: Assign the most common class among those K nearest neighbors to the new data point.
3. Key Considerations:
Distance measures: Euclidean distance is common, but other measures can be used depending on the data type and domain.
Choosing K: Experiment with different K values to find the one that gives the best accuracy. Consider using a validation set for this purpose.
Overfitting vs. underfitting: Too small a K can lead to overfitting (modeling noise), while too large a K can lead to underfitting (missing important patterns).
4. Applications:
Classification problems (e.g., customer segmentation, spam detection, image recognition)
Regression problems (e.g., predicting house prices)
5. Advantages:
Simple to understand and implement
Effective for non-linear relationships
No model training required (lazy learning)
6. Disadvantages:
Computationally expensive for large datasets (calculating distances for every new data point)
Sensitive to noisy data and outliers
Feature scaling can be important (especially for Euclidean distance)
Understanding KNN:
Classification algorithm: Assigns new data points to classes based on similarity to existing labeled points.
Core assumption: Similar data points are close together in the feature space.
How KNN Works:
Choose a value for K: The number of nearest neighbors to consider.
Calculate distance to neighbors: Measure the distance between the new data point and each training data point.
Identify K nearest neighbors: Find the K points with the smallest distances.
Predict class: Assign the most common class among the K nearest neighbors.
Key Considerations:
Distance measures: Commonly Euclidean distance, but others exist (e.g., Manhattan, Minkowski). Choose based on data type and domain.
Choosing K: Experiment with different K values using a validation set to find the best accuracy.
Overfitting vs. underfitting:
Too small K can lead to overfitting (modeling noise).
Too large K can lead to underfitting (missing patterns).
Feature scaling: Often essential, especially for Euclidean distance, to ensure features contribute equally to distance calculations.
Applications:
Classification: Customer segmentation, spam detection, image recognition, etc.
Regression: Predicting continuous values (e.g., house prices) by using the average or median of nearest neighbors' target values.
Advantages:
Simple to understand and implement.
Effective for non-linear relationships.
No model training required (lazy learning).
Disadvantages:
Computationally expensive for large datasets (calculating distances for every new point).
Sensitive to noisy data and outliers.
Feature scaling can be crucial.
Additional Insights:
Consider using data normalization or standardization for feature scaling.
Explore techniques for handling imbalanced classes.
Experiment with different distance metrics to find the best fit for your data.
Consider using weighted KNN to give more importance to closer neighbors.
For large datasets, consider using approximate nearest neighbor algorithms to reduce computational cost.
This covers three important evaluation metrics for classifiers: Jaccard index, F1-score, and Log Loss. Here's a breakdown of the key points:
Evaluation metrics are crucial for understanding the performance of classifiers.
We focus on metrics used for classification tasks, like predicting customer churn.
1. Jaccard Index:
Measures the similarity between true and predicted labels.
Calculated as the intersection of label sets divided by their union.
Higher Jaccard index indicates better accuracy.
2. Confusion Matrix:
Visualizes the performance of a classifier for each class.
Shows True Positives, True Negatives, False Positives, and False Negatives.
Useful for interpreting precision and recall for each class.
3. Precision and Recall:
Precision: measures the accuracy of positive predictions (True Positives / (True Positives + False Positives)).
Recall: measures the completeness of positive predictions (True Positives / (True Positives + False Negatives)).
4. F1-Score:
Harmonic mean of precision and recall, combining both metrics into one measure.
Higher F1-score indicates better overall performance for a class.
5. Log Loss:
Measures the performance of classifiers with probability outputs (e.g., logistic regression).
Penalizes predictions that are far from the actual label.
Lower Log Loss indicates better accuracy.
Additional Insights:
Jaccard and F1-score can be used for multi-class classification (not covered in the video).
Confusion matrix helps identify class imbalances and model biases.
Choosing the right metric depends on the specific problem and data characteristics.
Overall, this video provides a clear and concise introduction to three important evaluation metrics for classifiers. Understanding these metrics is essential for building and evaluating effective models in various classification tasks.
examples to illustrate KNN in action:
Example 1: Classifying Customer Service Preferences
Data: Customer data with age, income, region, and preferred service plan (Basic, E, Plus, Total).
Goal: Predict the preferred service plan for a new customer based on their age and income.
Steps:
Choose K (e.g., K = 5).
Calculate the Euclidean distance between the new customer and each existing customer in the dataset.
Identify the 5 customers with the smallest distances (nearest neighbors).
Count the most common service plan among those 5 neighbors (e.g., 3 out of 5 have "Plus").
Predict "Plus" as the preferred service plan for the new customer.
Example 2: Predicting House Prices
Data: House data with features like number of rooms, square footage, age, and price.
Goal: Predict the price of a new house with known features.
Steps:
Choose K (e.g., K = 3).
Calculate distances between the new house and all houses in the dataset.
Identify the 3 nearest neighbor houses.
Calculate the average or median price of those 3 houses.
Predict the average or median price as the estimated price for the new house.
Example 3: Image Recognition
Data: Pixel values of images labeled as "cat" or "dog."
Goal: Classify a new image as "cat" or "dog."
Steps:
Calculate distances between the new image's pixel values and all labeled images.
Identify the K nearest neighbor images.
Assign the most common label among those neighbors to the new image.
Decision Trees: A Powerful Tool for Classification
A decision tree is a powerful and versatile tool used in classification and prediction tasks. Imagine it as a flowchart-like structure that guides you towards a decision based on a series of questions. Each question, represented by a node, assesses a specific feature of the data. Based on the answer, you follow a branch to the next node, ultimately reaching a leaf node that holds the predicted outcome or class.
Here's a detailed breakdown of the key aspects of decision trees:
Structure:
Nodes: Represent decision points, usually asking a question about a specific feature.
Branches: Represent possible answers to the question, leading to different nodes.
Leaf nodes: Represent the final predictions or classifications, terminating the decision path.
Building a Decision Tree:
Data Preparation: Identify the target variable you want to predict (e.g., customer churn, loan default) and the relevant features in your data (e.g., age, income, credit score).
Attribute Selection: Choose the best attribute to split the data at each node. This often involves calculating measures like information gain or gini impurity, which assess how effectively an attribute separates the data into distinct classes.
Recursive Splitting: Repeat the attribute selection and branching process at each new node until reaching a stopping criterion (e.g., reaching pure leaf nodes, maximum tree depth).
Applications:
Classification: Predicting categorical outcomes (e.g., email spam, credit card fraud).
Regression: Predicting continuous values (e.g., house price, stock market prices).
Rule Extraction: Extracting human-readable rules from the tree structure for interoperability.
Advantages:
Disadvantages:
Overfitting: Prone to overfitting if not properly pruned or regularized.
Greedy splitting: May not find the globally optimal solution due to local decision-making at each node.
High dimensionality curse: Performance can deteriorate with a large number of features.
Overall, decision trees are a powerful and versatile tool for classification and prediction problems. Their simplicity, interpretability, and robustness make them popular choices in various domains. However, it's important to be aware of their limitations and address potential issues like overfitting through proper techniques.
1. Specific Data and Target:
Please provide details about the attributes (features) you're considering and the target variable you're trying to predict.
2. Decision Tree Algorithm:
Different algorithms use different measures for attribute selection. Knowing the algorithm you're using will help me provide accurate information.
3. Desired Outcome:
Are you aiming for maximum accuracy, interpretability, or another objective? This will influence the choice of attribute selection measure.
Once I have this information, I can explain the appropriate attribute selection measures and help you determine the best attribute for your specific decision tree.
Here are some common attribute selection measures, along with factors to consider:
1. Information Gain:
Measures how much uncertainty is reduced by splitting on an attribute.
Prefers attributes that create purer subsets (with more distinct class labels).
2. Gini Impurity:
Measures how often a randomly chosen sample would be incorrectly labeled if it was randomly classified based on the distribution of labels in the subset.
Prefers attributes that create subsets with more consistent class labels.
3. Gain Ratio:
Normalizes information gain to account for attributes with many possible values.
Prevents bias towards attributes with high cardinality.
Other Considerations:
Feature Importance: Some algorithms can directly calculate feature importance, indicating their overall contribution to prediction.
Correlation: Avoid highly correlated attributes, as they provide redundant information.
Domain Knowledge: Incorporate expert knowledge to guide attribute selection when appropriate.
Measures of Impurity:
Entropy: Quantifies randomness or uncertainty in a node. Lower entropy means more purity.
Information Gain: Measures the decrease in entropy after a split. Higher information gain indicates a better attribute for splitting.
Process:
Calculate entropy of the root node.
For each attribute, calculate entropy of the child nodes after splitting.
Calculate information gain for each attribute.
Choose the attribute with the highest information gain.
Repeat the process for each new node until a stopping criterion is met.
Example:
In the drug response prediction scenario, "sex" was initially chosen over "cholesterol" because it had higher information gain, leading to purer nodes.
Additional Insights:
Consider other attribute selection measures like Gini impurity.
Avoid overly deep trees to prevent overfitting.
Use techniques like pruning to simplify trees and improve generalization.
Incorporate domain knowledge to guide attribute selection when appropriate.
Regression Trees
1. Purpose:
Regression trees are used for predicting continuous numerical values (like prices, quantities, or measurements), rather than discrete categories.
They achieve this by splitting the data into groups based on features, and then predicting an average value for each group.
2. Building the Tree:
Criterion: Regression trees use a criterion like Mean Absolute Error (MAE) to guide the splitting of data. The goal is to minimize the error in predictions.
Categorical Features: Features with distinct categories (like "Near Water: Yes/No") are handled by calculating the average value for each category.
Numerical Features: Features with numerical values (like "Age") require finding the best split point that minimizes MAE. This involves trying different split points between data points.
3. Stopping Criteria:
Tree depth: Limit the depth of the tree to prevent overfitting.
Number of samples on a branch: Avoid splits that create too few samples on a branch.
Number of samples on each branch if another decision is made: Ensure enough samples for meaningful splits.
4. Example:
The example illustrated how a regression tree was built to predict house prices based on "Age" and "Near Water" features.
The tree's final structure involved splits at "Age < 35" and "Near Water: Yes/No", with average house prices predicted for each resulting group.
Key Points:
Regression trees are a powerful tool for predicting continuous values.
Building them involves careful consideration of features, split points, and stopping criteria.
Understanding these concepts is essential for effective use of regression trees in data analysis and machine learning.
Here's a code example in Python using scikit-learn for building a regression tree:
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
# Load the housing data
data = pd.read_csv("housing_data.csv")
# Separate features (X) and target variable (y)
X = data[["Age", "Near_Water"]]
y = data["Price"]
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
# Create a regression tree model
reg_tree = DecisionTreeRegressor(criterion="mae", max_depth=2) # Specify MAE criterion and max depth
# Train the model on the training data
reg_tree.fit(X_train, y_train)
# Make predictions on the testing data
y_pred = reg_tree.predict(X_test)
# Evaluate model performance using MAE
mae = mean_absolute_error(y_test, y_pred)
print("Mean Absolute Error:", mae)
Import necessary libraries:
pandas for data manipulation
DecisionTreeRegressor for creating the tree model
train_test_split for splitting data
mean_absolute_error for evaluation
Load and prepare data:
Load the CSV file containing housing data.
Separate features (Age, Near Water) and target variable (Price).
Split data:
Divide data into training and testing sets for model training and evaluation.
Create and train model:
Create a DecisionTreeRegressor object, specifying MAE as the splitting criterion and a maximum depth of 2 to prevent overfitting.
Train the model on the training data.
Make predictions:
Use the trained model to predict house prices on the testing data.
Evaluate performance:
Calculate the Mean Absolute Error (MAE) between predicted and actual prices to assess model accuracy.
Image of the resulting regression tree (assuming the same data as in the previous text example):
What is logistic Regression
Logistic regression is a statistical technique used to analyze the relationship between one or more independent variables and a binary dependent variable. In simpler terms, it helps you predict the probability of an event happening, like whether an email is spam or not, whether a patient has a disease or not, or whether a customer will churn or not.
how it works:
Model the data: Imagine you have data on a bunch of emails, with some labelled as spam and others as not spam. Logistic regression builds a model that takes into account the features of each email (like sender, keywords, etc.) and tries to predict the probability of it being spam.
Sigmoid function: This model uses a special function called the sigmoid function, which squishes any real number between 0 and 1. This is important because probabilities must always be between 0 and 1.
Decision threshold: Once the model predicts a probability for each email, you need to decide at what probability you want to classify it as spam. For example, you might choose a threshold of 0.5, so any email with a predicted probability of being spam above 0.5 is classified as spam, and any email below 0.5 is not spam.
Logistic regression sigmoid function
Logistic regression is a powerful tool for many reasons:
Interpretability: Unlike some other machine learning algorithms, logistic regression is relatively easy to interpret. You can look at the coefficients of the model to see which features have the most impact on the predicted probability.
Versatility: Logistic regression can be used for a variety of tasks, from classification to regression.
Simplicity: Logistic regression is a relatively simple algorithm to implement, making it a good choice for beginners.
However, logistic regression also has some limitations:
Assumes linearity: Logistic regression assumes that the relationship between the independent and dependent variables is linear. This may not be the case for all data sets.
Sensitive to outliers: Logistic regression can be sensitive to outliers in your data.
Not for multi-class problems: Logistic regression is typically used for binary classification problems. If you have more than two classes, you may need to use a different algorithm.
Overall, logistic regression is a versatile and powerful tool that can be used for a variety of tasks. It's a good choice for beginners because it's relatively simple to implement and interpret. However, it's important to be aware of its limitations and to choose the right algorithm for your specific problem.
interpreting logistic regression
Understanding the Key Metrics:
Coefficients (Beta values):
Sign: Indicates whether the independent variable has a positive or negative relationship with the probability of the event.
Magnitude: Reflects the strength of the relationship. Larger magnitudes suggest stronger impacts.
Odds Ratios (OR):
Exponentiated coefficients for easier interpretation.
Represent the change in odds of the event occurring for a one-unit increase in the independent variable.
OR > 1: Increased odds of the event.
OR < 1: Decreased odds of the event.
Statistical Significance (p-values):
Indicate whether a coefficient is likely to be zero due to chance or has a meaningful impact.
p-value < 0.05 is commonly used as the threshold for significance.
Goodness of Fit:
Assesses how well the model fits the data.
Measures like Hosmer-Lemeshow test or R-squared (interpreted differently than in linear regression).
Confusion Matrix:
Compares predicted outcomes with actual outcomes.
Measures accuracy, precision, recall, and other performance metrics.
Additional Considerations:
Interactions: Logistic regression can model interactions between independent variables.
Non-linear Relationships: Techniques like polynomial terms or splines can capture non-linear patterns.
Interpretation Process:
Examine coefficients and odds ratios:
Identify relationships and effect sizes.
Assess statistical significance:
Determine which variables have meaningful impacts.
Evaluate goodness of fit:
Ensure the model accurately represents the data.
Analyze confusion matrix:
Assess model performance in predicting outcomes.
Consider interactions and non-linear relationships:
If relevant to the problem domain.
Remember:
Contextualize: Interpret results in the context of the problem.
Practical Significance: Consider practical implications alongside statistical significance.
Model Assessment: Evaluate fit and performance using appropriate metrics.
Overfitting: Avoid overfitting and ensure generalizability.
Linear regression vs logistic regression
Linear regression: Predicts a continuous numerical value (e.g., house prices, product sales, exam scores).
Logistic regression: Predicts a binary categorical value (e.g., spam/not spam, customer churn/not churn, disease presence/absence).
Linear regression: Produces a straight line equation that best fits the data.
Logistic regression: Produces an S-shaped curve (sigmoid function) that maps input values to probabilities between 0 and 1.
Assumptions:
Linear regression: Assumes a linear relationship between independent and dependent variables.
Logistic regression: Assumes a linear relationship between independent variables and the log odds of the dependent variable.
Equation:
Linear regression: Y = β0 + β1X1 + β2X2 + ... + ε
Logistic regression: log(p/(1-p)) = β0 + β1X1 + β2X2 + ... + ε
Applications:
Linear regression:
Predicting house prices based on square footage, number of rooms, etc.
Estimating student grades based on study hours, test scores, etc.
Forecasting sales based on advertising spending, product features, etc.
Logistic regression:
Classifying emails as spam or not spam.
Predicting customer churn (whether a customer will leave a service).
Diagnosing diseases based on symptoms and test results.
Evaluation:
Linear regression: Uses R-squared, mean squared error (MSE), root mean squared error (RMSE) to evaluate model fit.
Logistic regression: Uses Hosmer-Lemeshow test, confusion matrix (accuracy, precision, recall), ROC curve, AUC to evaluate performance.
Types of Logistic Regression
Logistic regression is a powerful tool for classification problems, but it comes in different forms to handle various scenarios. Here are the three main types:
1. Binary Logistic Regression
This type is used for problems with two possible outcomes, like spam/not spam, win/lose, or click/not click.
- Dependent variable: Binary (0 or 1)
- Output: Sigmoid function predicting probability of event
- Applications: Spam detection, disease diagnosis, click prediction
2. Multinomial Logistic Regression
This type handles problems with multiple unordered categories, like classifying handwritten digits or predicting blood type.
- Dependent variable: Categorical (3+ values)
- Output: Separate sigmoid functions for each category
- Applications: Handwritten digit recognition, blood type prediction, credit risk assessment
3. Ordinal Logistic Regression
This type is used when the dependent variable has multiple ordered categories, like student grades, movie ratings, or disease severity.
- Dependent variable: Ordinal (ranked order)
- Output: Sigmoid function for probabilities, focusing on ordering
- Applications: Student grade prediction, movie rating analysis, disease stage classification
Choosing the Right Type
The appropriate type depends on the nature of your problem, the number of categories, and whether they're ordered or unordered. Consider the assumptions and interpretations of each type when selecting your model.
What is an SVM?
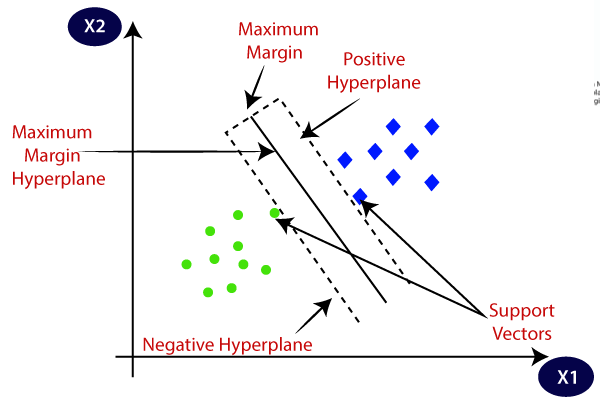
Support Vector Machines (SVMs) are powerful supervised learning algorithms used for classification and regression tasks. Imagine you have a dataset of apples and oranges, and you want to create a rule to tell them apart. An SVM would find the best line or plane in your data that separates the apples from the oranges with the largest possible margin. This line or plane is called the hyperplane.
Understanding Support Vector Machines (SVM)
Data Representation:
- Each data point is represented as a vector in a high-dimensional space.
- Think of it as plotting each data point based on its features, like size, color, and sweetness for our apples and oranges.
Finding the Optimal Hyperplane:
- The algorithm searches for the hyperplane that maximizes the margin between the closest data points of each class, also known as support vectors.
- These support vectors are the most important points in your data, as they define the decision boundary.
Classification of New Data:
- Once the hyperplane is established, new data points can be classified by simply determining on which side of the hyperplane they fall.
- If they fall on the apple side, they're classified as apples, and if they fall on the orange side, they're classified as oranges.
What makes SVMs special?
- SVMs are special because of their ability to find the optimal hyperplane that maximizes the margin between different classes, leading to better generalization to new, unseen data.
- They focus on the most critical data points, the support vectors, in defining the decision boundary, making them robust against outliers.
- SVMs are effective in high-dimensional spaces, making them suitable for various applications in machine learning.
SVM Algorithm Explanation
1. Class Labeling:
The first step involves assigning labels to the classes in your data. Typically, one class is assigned a label of +1 and the other class a label of -1. This simplifies the calculation of the decision boundary during optimization.
2. Maximizing Margin with Hinge Loss:
The SVM aims to find the hyperplane that creates the widest possible margin between the data points labeled as +1 and those labeled as -1. To achieve this, the algorithm uses a loss function called the hinge loss. Minimizing the hinge loss encourages the algorithm to find the hyperplane with the largest margin.
3. Balancing Margins and Errors with Regularization:
Maximizing the margin alone can lead to overfitting. To avoid this, a regularization parameter is introduced. This parameter penalizes the complexity of the model, encouraging it to find a simpler hyperplane that generalizes better to unseen data.
4. Gradient Descent for Optimization:
To find the optimal hyperplane, the algorithm uses an optimization technique called gradient descent. It iteratively updates the weights of the hyperplane by calculating the gradients of the loss function with respect to each weight.
5. Combining Loss and Regularization for Gradient Updates:
The gradient updates consider both the hinge loss and the regularization parameter. For correctly classified data points, only the regularization term contributes to the gradient update. For misclassified points, both the hinge loss and regularization contribute, pushing the hyperplane further away from misclassified points.
6. Final Step:
After several iterations of gradient descent, the algorithm converges to the optimal hyperplane, which can then be used to classify new data points.
Applications of Support Vector Machines (SVMs)
1. Image Recognition:
- Face detection and recognition in photos and videos.
- Object detection and classification in images, like identifying cars, animals, or buildings.
- Content-based image retrieval, filtering images based on specific features.
2. Text Classification:
- Spam filtering, automatically classifying emails as spam or not spam.
- Sentiment analysis, determining the emotional tone of text data, like positive, negative, or neutral.
- Topic modeling, automatically identifying themes and categories in text documents.
3. Bioinformatics:
- Gene expression analysis, classifying genes based on their function or disease association.
- Protein classification, predicting the function and structure of proteins.
- Drug discovery, identifying potential drug candidates based on their chemical properties.
4. Finance:
- Fraud detection, identifying fraudulent transactions in financial data.
- Credit scoring, assessing the creditworthiness of loan applicants.
- Market prediction, modeling trends and patterns in financial markets.
5. Other Applications:
- Handwriting recognition, recognizing handwritten text from scanned documents or images.
- Medical diagnosis, supporting clinical decision-making by analyzing medical data.
- Robotics, controlling the movement of robots based on sensory inputs.
These are just a few examples, and the potential applications of SVMs are constantly evolving. Their ability to handle high-dimensional data, effectively classify non-linear relationships, and resist overfitting makes them a versatile and powerful tool across various fields.
Advantages of SVMs:
- Effective in High Dimensions: SVMs excel at handling data with many features, making them suitable for complex problems like image recognition, text classification, and bioinformatics.
- Robust to Overfitting: By maximizing the margin between classes, SVMs are less prone to overfitting, which is when the model memorizes the training data but performs poorly on unseen examples.
- Kernel Trick: For non-linearly separable data, SVMs can utilize the kernel trick to effectively project the data into a higher-dimensional space where it becomes linearly separable. This allows them to tackle complex, non-linear relationships within the data.
- Interpretability: Compared to black-box models like Neural Networks, SVMs offer some level of interpretability through the support vectors and the decision boundary, providing insights into why certain data points are classified in a specific way.
- Memory Efficiency: When dealing with smaller datasets, SVMs can be more memory-efficient than other algorithms, making them a good choice for resource-constrained environments.
Disadvantages of SVMs:
- Computationally Expensive: Training an SVM can be computationally expensive, especially for large datasets, as it involves finding the optimal hyperplane in a high-dimensional space.
- Sensitive to Choice of Kernel and Parameters: Choosing the right kernel and optimization parameters can significantly impact the performance of an SVM. Tuning these parameters can be challenging and time-consuming.
- Not the Best for Large Datasets: While efficient for smaller datasets, SVMs can become computationally intensive and slow for large datasets. Other algorithms might be more efficient in such cases.
- Limited to Binary Classification: Although extensions exist, SVMs are primarily designed for binary classification problems. Handling multi-class problems might require additional techniques or adaptations.
- Difficulties with Missing Data: SVMs typically require complete datasets and may not perform well when dealing with missing values. Imputing or preprocessing missing data might be necessary for optimal performance.
Overall, SVMs offer a powerful and versatile tool for tackling complex classification problems, particularly in high-dimensional spaces. However, it's important to consider their computational demands, sensitivity to parameters, and limitations in certain circumstances before choosing them for your specific application.
